Moleküler Mekaniğin Temel Taşı: Kuvvet Alanları - 1

Moleküler modelleme, atomlar arası etkileşimleri sayısal olarak tanımlayarak doğadaki fiziksel süreçleri bilgisayar ortamında canlandırmayı amaçlamaktadır. Bu sürecin temel yapı taşlarından biri olan kuvvet alanları (force fields), atomların birbirleriyle nasıl etkileştiğini belirleyen matematiksel fonksiyonlar ve parametrik sabitler bütünüdür. Kuvvet alanları sayesinde moleküllerin geometrisi optimize edilir. Bu optimizasyon sürecinde bağlar esnetilir, açılar bükülür ve sistemin enerjisi hesaplanır. Ancak bir kuvvet alanının doğruluğu, kullanılan parametrelerin kalitesiyle doğrudan ilişkilidir. İşte bu noktada devreye parametrizasyon süreci girer. Deneysel verilerden veya kuantum kimyasal hesaplamalardan elde edilen bilgilerle bu parametreler uyumlu hale getirilir. Bu yazıda, kuvvet alanlarının temel prensiplerini ve kuvvet alanında kullanılan parametreleri detaylıca ele alacağız.

Kuvvet Alanları

Çoğu klasik kuvvet alanı, basit fiziksel bir açıklama ile beş temel unsura dayanmaktadır. Bu unsurlar; bağların deformasyonu ve açı geometrisi (gerilme ve bükülme açıları) ile bağlantılı potansiyel enerji öğeleri, belirli dihedral açılar (burulmalar) etrafında döngüyü temsil eden terimlerdir. Ayrıca, elektrostatik etkileşimleri tanımlayan serbest terimler, dispersiyon etkileşimleri ve itme ile ilgili terimler (örneğin van der Waals kuvvetleri) bulunmaktadır. Bir kuvvet alanı ise potansiyel enerjiyi ve ilgili parametreleri modellemek için seçilmiş denklemlerden oluşmaktadır (1). Kuvvet alanı, yapının (R) ve ilgilenilen sistemin enerjisi (U) ile ilişkisini tanımlamak için kullanılan potansiyel enerji fonksiyonudur. Ancak, potansiyel enerji fonksiyonu tek başına bir kuvvet alanı oluşturmaz. Bir kuvvet alanını veren aşağıda gösterildiği gibi potansiyel enerji fonksiyonunun bu fonksiyonda kullanılan parametreler ile olan birleşimidir (1).

Denklem (1)

Denklem (1), toplam potansiyel enerji fonksiyonu olarak adlandırılan şeyin bir örneğini vermektedir. Görüldüğü üzere denklem (1), moleküler yapıları tanımlayabilen minimal kuvvet kümesini temsil eden bir dizi basit fonksiyondan oluşmaktadır. Bağlar, açılar ve düzlem dışı distorsiyonlar (uygun olmayan dihedral açılar) harmonik olarak ele alınır ve dihedral veya burulma rotasyonları sinüzoidal bir terimle tanımlanmaktadır.

Atomlar arasındaki etkileşimler, Coulombic terimi aracılığıyla işlemden geçirilen elektrostatik etkileşimlerle birleştirilmiş atom-atom itme ve dağılım etkileşimlerini tanımlamak için 12–6 Lennard-Jones (LJ) terimini kullanmaktadır. Denklem (1)’de b bağ uzunluğudur; Θ değerlik açısıdır, χ dihedral açısıdır, ϕ uygun olmayan açıdır ve rij i ve j atomları arasındaki mesafedir. Gerçek kuvvet alanını temsil eden terimler olan parametreler, sırasıyla bağ kuvveti sabitini ve denge mesafesini (K_b ve b₀'ı) içerir; sırasıyla valans açısı kuvvet sabiti ve denge açısı, K ve Θ; dihedral kuvvet sabiti, çokluk ve faz açısı, sırasıyla Kχ, n ve δ ve sırasıyla uygun olmayan kuvvet sabiti ve denge uygun olmayan açısı, K ve ϕ₀’dır (1).

Toplu olarak bunlar, molekül içi parametreleri temsil etmektedir. i ve j atomları arasındaki bağlı olmayan parametreler, van der Waals (vdW) etkileşimlerini için kullanılan kısmi atomik yükler, qi ve LJ potansiyel kuyunun derinliğini, ve minimum etkileşim yarıçapını içermektedir.

Molekül İçi Parametreler (Bağlı Etkileşimler)

Bağ Uzunluğu Potansiyelleri

Bağ uzunluğu potansiyelleri, referans değerler etrafındaki küçük ölçekli sapmaları modelleyen “gerilim” (strain) terimleri olarak kabul edilebilir. Farklı kimyasal bağlara ait referans değerler, X-ışını kristal yapılarından veya küçük moleküllerin denge yapılarına yönelik kuantum mekaniksel çözümlerden elde edilebilir (2).

1. Harmonik Terim

Hooke Yasası'ndan faydalanarak modellenen harmonik potansiyel, bağ deformasyonlarını tanımlamak için kullanılan en basit moleküler mekanik yaklaşımıdır. Hooke Yasası'na göre, kuvvet (F), yer değiştirme (x) ve ivme x ¨ ile orantılıdır. Bu ilişki şu şekilde ifade edilir:

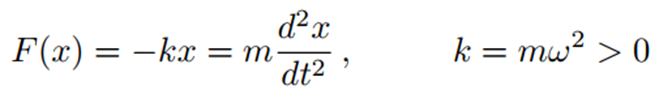
Bu nedenle açısal frekans ω (birim zamandaki radyan sayısı) ya da dairesel frekans ν’nun 2π katı (burada ν=c/λ, c ışık hızı ve λ dalga boyudur), yay sabiti k ile şu şekilde ilişkilidir:

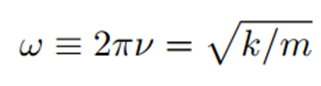
İlgili potansiyel enerji (E) ise şu şekildedir:

Daha genel olarak, bu harmonik bağ potansiyelini şu şekilde yazabiliriz:

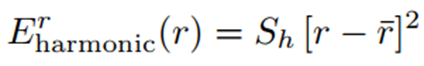
Burada r bağ uzunluğunu, rˉ referans (denge) bağ uzunluğunu ve S_h​ sabit bir katsayıyı ifade eder. Harmonik potansiyel, yalnızca referans değerlerden küçük sapmalar için yeterlidir. Bu genellikle temel durumun bir titreşim seviyesi üzeri ya da yaklaşık 0.1 Å veya daha az uzunluk deformasyonları içindir. Daha büyük sapmalar için geçerli değildir çünkü bu durumda atomlar ayrışır ve artık etkileşime girmez. Bu nedenle enerji, mesafe rˉ’nin ötesine geçtikçe hızla artmak yerine sabitlenir. Ancak çok küçük etkileşim mesafelerinde deformasyon enerjisi çok büyüktür (2).

2. Morse Terimi

Denge durumları etrafındaki çok küçük dalgalanmaları aşan bağ deformasyonlarını modellemek için, P.M. Morse tarafından geliştirilen ampirik bağ potansiyeli (3), küçük moleküllerin titreşim seviyelerini yeniden üretmede oldukça başarılı olmuştur (4). Morse fonksiyonunun matematiksel formu şu şekildedir:

Ayarlanabilir parametreler olan S_m​ ve D, sırasıyla potansiyel kuyusunun genişliğini ve derinliğini tanımlamaktadır. Morse potansiyeli bağ uzunluğunun kısalması durumunda enerjinin hızla artmasını doğru şekilde yansıtır (r→0 iken E(r)→∞), ancak büyük r değerlerinde enerji seviyelenerek ayrışma enerjisi olan D’ye yaklaşır: r→∞ iken r: E(r)→D

Şekil 1. HBr bileşiği için Morse, harmonik, kübik ve iki farklı dördüncü dereceden (kuartik) bağ potansiyeli (2).

3. Kübik ve Kuartik Terimler

Harmonik potansiyelle elde edilebilenin ötesinde Morse potansiyellerini daha iyi bir şekilde yeniden üretmek için, kübik ve kuartik polinomlar kullanılabilir (bunlar, ikinci dereceden potansiyele eklenen terimler aracılığıyla). Örneğin, MM3 kuvvet alanı, çoğu molekül için iyi çalışan kübik ve kuartik bağ potansiyelleri kullanmaktadır (5). Merck kuvvet alanı olan MMFF (6), bir kuartik bağ fonksiyonu kullanır. Bağ uzunluğu potansiyel fonksiyonunun şeklinin daha iyi optimize edilmesi için polinomun katsayıları ayarlanabilir.

Büyük molekül kuvvet alanları için, hesaplama süresinin önemli olduğu durumlarda, karekök hesaplamalarından kaçınmak amacıyla özel bir kuartik potansiyel önerilmiştir (7); bu, kareli bağ farklarının karesini şu şekilde ölçer:

Bağ Açısı Potansiyelleri

Bir moleküldeki her atom etrafındaki bağ açıları, atom etrafındaki orbitallerin hibritleşmesiyle belirlenmektedir (hibritleşme ile ilgili daha fazla detaya bu linke tıklayarak ulaşabilirsiniz). Bu kural, bağ açısı geometrileri için ilk tahmin olarak hizmet eder. Ancak, bu tahminlerden küçük sapmalar meydana gelir ve bazen büyük sapmalar da oluşur. Bir moleküldeki farklı bağ açıları arasında 1–2°'lik küçük farklar bile, riboz gibi moleküler yapı üzerinde önemli küresel etkilere sahip olabilir (2).

1. Harmonik ve Trigonometrik Terimler

Yaygın olarak kullanılan bağ-açı potansiyelleri, açılar ve açı kosinüsleri arasındaki farkı içeren harmonik fonksiyonlardır. Aşağıdaki denklemler ile tanımlanabilir.

Trigonometrik potansiyelin avantajı, sınırlı olması ve kolayca uygulanıp türevlenebilmesidir. Bunun nedeni, ters trigonometrik fonksiyonların hesaplanmasına gerek olmaması ve doğrusal bağ açıları için ortaya çıkabilecek tekillik (singularity) problemlerinin önlenebilmesidir.

Şekil 2. Bir C–C–C bağ açısı (CHARMM’de CA–CA–CA atom dizilimi) için harmonik bağ-açı potansiyelleri (2).

2. Bağ Uzaması / Açı Bükülmesi Arası Çapraz Terimler

Küçük moleküler sistemlere yönelik kuvvet alanlarında (örneğin; MM3 ve MM4) çapraz terimler sıklıkla kullanılır. Bu durum, bağ uzunluğu ve bağ açısı değerlerindeki telafi edici eğilimleri daha doğru modellemek içindir. Bu çapraz terimler, bağ uzunluğu ve bağ açısı potansiyellerine düzeltme terimleri olarak kabul edilmektedir. Örneğin, bağlı atom dizilimi abc için bir uzama/bükülme (stretch/bend) terimi, θ_abc açısı azaldıkça a–b ve b–c bağ uzunluklarının artmasına veya θ_ijk açısı arttıkça bu bağ uzunluklarının azalmasına izin verir. Bir bükülme/bükülme (bend/bend) potansiyeli ise aynı atom etrafında bulunan iki açının bükülme titreşimlerini uygun şekilde birbiriyle ilişkilendirmektedir. Böylece ilgili frekanslar ayrıştırılarak deneysel titreşim spektrumlarıyla daha iyi uyum sağlanabilir (5). Bu korelasyonlar, abc dizilimleri için uzama/uzama (stretch/stretch), bükülme/bükülme (bend/bend) ve uzama/bükülme (stretch/bend) potansiyelleriyle modellenebilir. Burada r ve r′ uzaklıkları sırasıyla ab ve bc bağlarıyla ilişkilidir ve θ ise abc bağ açısını temsil eder (2).

Torsiyonel Potansiyeller

1. Fourier Terimleri

Her esnek torsiyon açısı (τ) için kullanılan genel fonksiyon, n’nin bir tam sayı olduğu şu biçimdedir:

Torsiyon açısı τ ile tanımlanan her bir torsiyonel dizilim için, n tam sayısı dönme (rotational) bariyerinin periyodunu, V_n ise buna karşılık gelen bariyer yüksekliğini ifade etmektedir. Her bir torsiyonel serbestlik derecesi için kullanılan n değeri, atom dizilimine ve kuvvet alanı parametrelendirmesine bağlıdır. n için tipik değerler 1, 2, 3 (bazen 4) olup bazı kuvvet alanlarında (örneğin CHARMM (8)) ek olarak n = 5, 6 gibi diğer değerler de kullanılır. Formüle ayrıca bir referans torsiyon açısı τ₀ da dahil edilebilir.

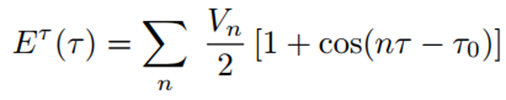
NMR, IR (Kızılötesi Işınım), Raman ve mikrodalga gibi çeşitli spektral bölgeler için uygun spektroskopik yöntemlerle elde edilen deneysel veriler, düşük molekül ağırlıklı bileşiklerde bariyer yüksekliklerini ve periyotlarını tahmin etmek için kullanılabilir. Nükleik asitler ve proteinlerdeki çeşitli tekli bağlar etrafındaki dönmelere ilişkin bariyerler deneysel olarak elde edilemediğinden, bunlar düşük molekül ağırlıklı bileşiklerdeki benzer kimyasal dizilimlerden tahmin edilmelidir (2).

Bu yazıda, moleküler modellemenin temel yapı taşlarından biri olan kuvvet alanlarının iç yapısını ve özellikle bağ uzunluğu ile açı bükülmesi gibi içsel parametrelerini detaylı bir şekilde ele aldık. Kuvvet alanlarının doğruluğu ve etkinliği, kullanılan parametrizasyonun kalitesine doğrudan bağlıdır. Bu nedenle hem teorik hem de deneysel verilerden yararlanılarak parametrelerin dikkatlice optimize edilmesi büyük önem taşır. Yazının sonraki bölümünde ise moleküller arasındaki bağsız kuvvetler (van der Waals etkileşimleri ve elektrostatik kuvvetler) konusuna odaklanarak bu etkileşimlerin moleküler modellemedeki rolünü detaylandıracağız.

Referanslar

1. Mackerell A. D., Jr (2004). Empirical force fields for biological macromolecules: overview and issues. Journal of computational chemistry, 25(13), 1584–1604. https://doi.org/10.1002/jcc.20082

2. Schlick, T. (2010) Molecular Modeling and Simulation: An Interdisciplinary Guide. 2nd Edition, Springer, Berlin. https://doi.org/10.1007/978-1-4419-6351-2 

3. Morse, P. M. (1929). Diatomic molecules according to the wave mechanics. II. Vibrational levels. Physical review, 34(1), 57.

4. Slater, N. B. (1957). Classical motion under a Morse potential. Nature, 180(4598), 1352-1353.

5. Allinger, N. L., Yuh, Y. H., & Lii, J. H. (1989). Molecular mechanics. The MM3 force field for hydrocarbons. 1. Journal of the American Chemical Society, 111(23), 8551-8566.

6. Halgren, T. A. (1996). Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. Journal of computational chemistry, 17(5‐6), 490-519. https://doi.org/10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P 

7. Schlick, T. (1989). A recipe for evaluating and differentiating cos ϕ expressions. Journal of computational chemistry, 10(7), 951-956. https://doi.org/10.1002/jcc.540100713 

8. MacKerell, A. D., Bashford, D., Bellott, M., Dunbrack, R. L., Evanseck, J. D., Field, M. J., Fischer, S., Gao, J., Guo, H., Ha, S., Joseph-McCarthy, D., Kuchnir, L., Kuczera, K., Lau, F. T., Mattos, C., Michnick, S., Ngo, T., Nguyen, D. T., Prodhom, B., Reiher, W. E., … Karplus, M. (1998). All-atom empirical potential for molecular modeling and dynamics studies of proteins. The journal of physical chemistry. B, 102(18), 3586–3616. https://doi.org/10.1021/jp973084f