Schrödinger Denklemi ve Atomik Orbitaller

Atom ve moleküllerin elektronik yapısını anlamak, modern kimya ve ilaç tasarımının temel taşlarından biridir. Bu yapıları açıklamak için geliştirilen Schrödinger denklemi, kuantum kimyasının merkezindedir ve hesaplamalı kimya yaklaşımlarının temelini oluşturmaktadır. Bu yazıda, Schrödinger denkleminin teorik temellerinden başlayarak atomik orbitallere, oradan da moleküller üzerinde gerçekleştirilen kuantum kimyasal hesaplamalar ele alınmıştır.

Schrödinger Denkleminin Temelleri

1926 yılında Erwin Schrödinger tarafından geliştirilen kuantum dalga denklemi, elektron gibi taneciklerin klasik mekanikle açıklanamayan davranışlarını tanımlamak için kullanılır. Zamandan bağımsız haliyle Schrödinger denklemi şu şekilde ifade edilir (1):

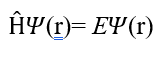
Burada şu terimler yer alır:

H: Hamiltonyen operatörü, sistemin toplam enerjisini temsil eder (kinetik + potansiyel enerji).

Ψ: Dalga fonksiyonu, taneciğin uzaydaki konumlarına bağlı olasılık genliğini verir.

E: Enerji değeridir, yani sistemin kuantize enerji seviyesi.

Bir elektron için Hamiltonyen şöyle yazılabilir:

Bu denklem, hidrojen atomu gibi tek elektronlu sistemlerde analitik olarak çözülebilir. Daha karmaşık sistemler içinse sayısal yaklaşımlar gereklidir.

Atomik Orbitaller ve Kuantum Sayıları

Hidrojen atomu için Schrödinger denkleminin analitik çözümleri, atomik orbitaller olarak bilinen dalga fonksiyonlarını verir. Bu orbitaller, elektronun uzaydaki olasılık dağılımını belirler. Schrödinger denkleminin küresel koordinatlarda çözümü, bu fonksiyonları radyal ve açısal bileşenler olarak ayırmamıza olanak tanır:

Rn,l(r) : Radyal dalga fonksiyonu

Yl,m(θ,ϕ) :Küresel harmonikler (açısal parça)

Bu ifade, elektron yoğunluğunun sadece bir noktadaki değerini değil, ayrıca uzaydaki genel yapısını da verir (2).

Kuantum Sayıların Anlamı

Orbitaller şu dört kuantum sayısıyla tanımlanır:

Ana kuantum sayısı (n): Elektronun bulunduğu enerji seviyesini belirtir. Elektronun çekirdeğe ortalama uzaklığını etkiler. n arttıkça orbitalin büyüklüğü artar.

Açısal momentum kuantum sayısı (l): Orbitalin geometrik şeklini belirler.

l = 0: s orbitali (küresel)

l = 1: p orbitali (loblu)

l = 2: d orbitali (çiçek benzeri)

l = 3: f orbitali (daha karmaşık)

Manyetik kuantum sayısı (ml): Orbitalin uzaydaki yönelimini tanımlar. ml, -1 ile +l arası tam sayılar alabilir. Spin kuantum sayısı (ms): Elektronun kendi ekseni etrafında dönme yönünü belirler. ms değer olarak +1/2 veya -1/2 olabilir.

Şekil 1. Artan Atom Numaralarına Sahip Orbitallerin Enerjisi (3).

Yaklaşık Yöntemler

Gerçek moleküller için Schrödinger denkleminin çözümü analitik olarak mümkün olmadığından, yaklaşık sayısal yöntemler kullanılır. Bunlar kuantum kimyadaki hesaplamaların temelini oluşturur:

Hartree-Fock (HF) Yaklaşımı

Bu yaklaşım, elektronların diğer elektronları ortalama bir potansiyel içinde gördüğü varsayımına dayanır. Tüm sistem için toplam dalga fonksiyonu, tek elektronluk orbitallerin determinantı (Slater determinant) olarak yazılır. Her elektron, sistemdeki diğer elektronların etkisini ortalama bir alan olarak deneyimler. Avantajı basitliği, dezavantajı ise elektron-elektron korelasyonunu yeterince hesaba katmamasıdır. Ancak pek çok sistem için başlangıç noktası olarak tercih edilir (4).

Şekil 2. Hartree-Fock yaklaşımı için örnek bir Slater determinantı (5).

Yoğunluk Fonksiyonel Teorisi (DFT)

DFT, sistemin enerji hesaplamasını elektron yoğunluğu üzerinden gerçekleştirir. Temel prensibi, elektron yoğunluğunun sistemin tüm temel özelliklerini belirlediğidir. Kuantum sistemleri tek bir dalga fonksiyonu yerine, bu yoğunluk üzerinden modellemeyi hedefler. Güncel fonksiyonel setleri (B3LYP, PBE vb.) sayesinde DFT, çok çekirdekli sistemlerde dahi etkin ve hızlı hesaplamalar yapar. In silico ortamda moleküllerin geometri optimizasyonu, elektron dağılımı, reaksiyon koordinatları gibi birçok parametre DFT ile elde edilir. DFT özellikle hesaplama-zaman dengesinde başarılı olduğu için ilaç tasarımı ve malzeme bilimi alanlarında yaygın kullanılır. Bu olasılık yoğunluğu, kimyasal bağların kurulmasının temelini oluşturur. İki atomik orbitalin faz uyumlu etkileşimi, bağlayıcı orbital oluştururken, zıt faz etkileşimi antibindirme orbitalini ortaya çıkarır. Bu fenomen, kovalent bağ oluşumu ve moleküllerin stabilitesinin kuantum seviyede anlaşılmasını sağlar. Aynı zamanda bu bilgiler, ligand–reseptör etkileşimlerinin moleküler düzeyde modellenmesinde de kullanılır. Schrödinger denklemine dayalı elektron yoğunluk haritaları, ilaç moleküllerinin hedef proteinle nasıl etkileşime gireceğini anlamakta vazgeçilmezdir (6).

Referanslar

1. Griffiths, D. J. (2005). Introduction to Quantum Mechanics. Pearson Education.

2. Atkins, P., & Friedman, R. (2011). Molecular Quantum Mechanics. Oxford University Press.

3. S. Ekambaram. (2012). General Chemistry. Pearson Education India.

4. Szabo, A., & Ostlund, N. S. (1996). Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover Publications.

5. Errol G. Lewars. (2010). Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer Science & Business Media.

6. McQuarrie, D. A. (2008). Quantum Chemistry. University Science Books.