Topography of the Chemical Universe: Potential Energy Surfaces

What is a Potential Energy Surface?

A potential energy surface (PES) is a multidimensional surface that represents the total energy values corresponding to the spatial positions of all atoms in a molecular system. Each point on this surface corresponds to a specific atomic configuration. The shape of this surface allows us to understand a molecule’s stability, transition states, and reaction pathways. In chemical reactions, the transformation of reactants into products occurs along a path on the PES; thus, the PES is a critical tool for elucidating reaction mechanisms (1).

For instance, in an acid-base reaction involving hydrogen transfer, the transition of a proton from one molecule to another can be modeled via a transition state on the PES. This provides a significant advantage for tracking how atoms move in molecular dynamics simulations. Therefore, the PES is not just a theoretical concept but the physical foundation behind directly observable molecular motions (2).

Born-Oppenheimer Approximation and the Construction of the Potential Energy Surface

The construction of a potential energy surface (PES) is based on the Born-Oppenheimer approximation (Figure 1). This approximation assumes that electrons move much more rapidly and are significantly lighter than nuclei, allowing the total wavefunction of the system to be separated into electronic and nuclear components. As a result, for each nuclear configuration, the electronic structure can be solved independently. This solution yields a potential energy function dependent on nuclear coordinates, which is the PES itself (3).

Figure 1. Born-Oppenheimer Approximation (4).

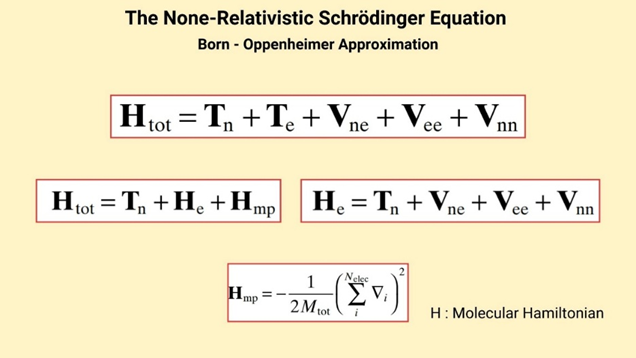
This separation has provided great convenience in computational chemistry. Once the electronic structures are solved, the positions of the nuclei are optimized to determine the minimum energy structure. Without the Born-Oppenheimer approximation, solving the many-body Schrödinger equation would be practically impossible. Therefore, this approach can be considered the cornerstone of modern quantum chemistry (4).

Structural Features of the Potential Energy Surface

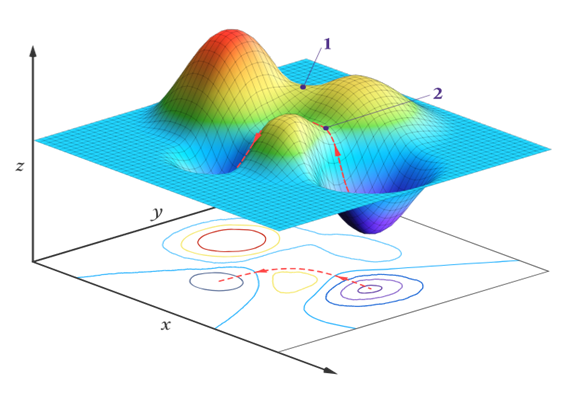
On a PES, the minimum points represent the stable structures of the system; these are regions where the energy gradient is zero and all eigenvalues of the Hessian matrix are positive. These correspond to actual molecular structures. Global minima represent the most stable state of the system, while local minima correspond to temporarily stable structures. On the other hand, points known as saddle points represent transition states. At these points, the energy gradient is zero, but at least one eigenvalue of the Hessian matrix is negative (5).

Stable Structures and Minimum Points

The minimum points on a PES represent the stable structures of the system. These points correspond to conformations where the potential energy of the molecular system is locally minimized. In a chemical reaction process, the structures of reactants and products are located at these minima (6).

Transition States and Energy Barriers

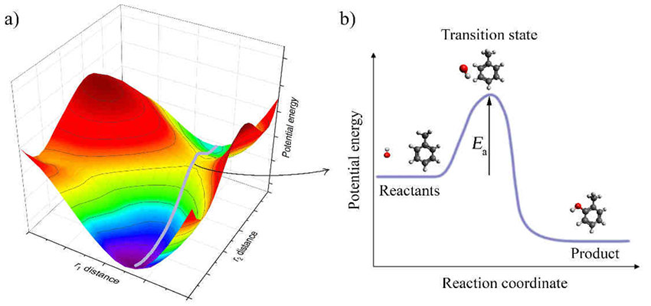
Transition states are the energy peaks along the lowest-energy path connecting two minima. These points are referred to as "saddle points" on the PES. The transition state is critically important for reaction kinetics, as the activation energy of a reaction is determined by the energy difference between the reactant minimum and the transition state (7). Therefore, understanding the mechanism of a chemical reaction requires identifying the minima and transition states on the potential energy surface and mapping the connections between them. This is achieved through minimum energy path (MEP) or intrinsic reaction coordinate (IRC) analysis (8).

Figure 2. A model potential energy surface illustrating a reaction pathway, with an example of a minimum and a transition state; b) the same surface represented in one dimension (9)

Forces and Gradient Calculations

Atomic forces within the system can be calculated through the mathematical derivatives of the PES. The force on an atom is the negative gradient of the potential energy with respect to that coordinate direction. These forces are used to perform energy minimizations. The Hessian matrix (the second derivative matrix) is employed to determine vibrational modes and to locate transition states. Force and gradient information play a crucial role in algorithms such as geometry optimization and transition state prediction (10).

Figure 3. A 2D contour map and potential energy surface for a hypothetical endothermic reaction (11).

These calculations are performed automatically by modern simulation software. For example, programs such as Gaussian or ORCA use both gradient and second derivative calculations to guide the system toward its global minimum. Additionally, in molecular dynamics simulations, force data serve as the fundamental input that determines how atoms move over time (12).

Vibrational Modes and Spectroscopic Interpretations 

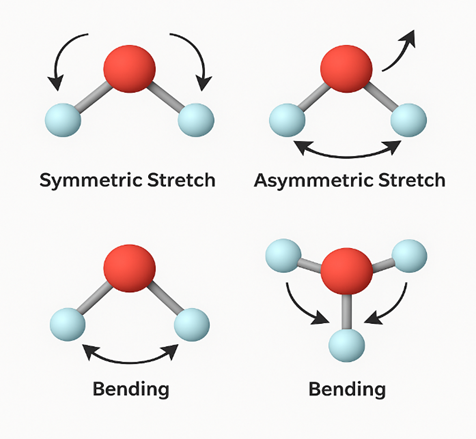
Small vibrations around a molecule’s equilibrium position on the PES can be modeled using the harmonic oscillator approximation. The normal modes obtained from this approach can be directly observed through techniques such as Infrared (IR) and Raman spectroscopy.

Each normal mode represents a collective motion of the molecule. Vibrational frequencies are linked to the eigenvalues of the Hessian matrix and depend on the local curvature of the PES (13). These vibrational modes are particularly useful for identifying unknown structures. For example, the characteristic vibration of a carbonyl (C=O) group appears around ~1700 cm⁻¹ and gives a distinct peak in the IR spectrum. Such spectroscopic analyses allow for the validation of experimental data with theoretical calculations (14).

Figure 4. Example of the fundamental vibrational modes of the H₂O molecule (Image generated using artificial intelligence).

Reaction Energy Profiles and Activation Energies

To fully understand a chemical reaction process, it is necessary to know not only the initial and final states but also the pathways in between. The potential energy surface clearly defines this path. Along the minimum energy path between reactants and products, the system surpasses the activation energy by passing through the transition state. Therefore, the kinetics and thermodynamics of a reaction are directly based on PES analysis. The highest energy point along this path is the transition state (saddle point), and the difference in energy between this point and the reactant minimum defines the activation energy. The kinetics of the reaction depend on this energy barrier. Quantitative analysis of such profiles is especially important in modeling radical reactions or photochemical processes (15).

References

1. Fukui, K. (1970). Formulation of the reaction coordinate. The Journal of Physical Chemistry, 74(23), 4161-4163.

2. Born, M., & Oppenheimer, R. (1927). Zur Quantentheorie der Molekeln. Annalen der Physik, 389(20), 457–484

3. Schlegel, H. B. (1982). Optimization of equilibrium geometries and transition structures. Journal of computational chemistry, 3(2), 214-218.

4. Jensen, F. (2017). Introduction to computational chemistry. John Wiley & Sons.

5. Eyring, H. (1935). The activated complex in chemical reactions. The Journal of chemical physics, 3(2), 107-115.

6. Fukui, K. (1981). The path of chemical reactions-the IRC approach. Accounts of chemical research, 14(12), 363-368.

7. Pople, J. A., & Beveridge, D. L. (1970). Molecular orbital theory. C0., NY.

8. Pulay, P. (2014). Analytical derivatives, forces, force constants, molecular geometries, and related response properties in electronic structure theory. Wiley Interdisciplinary Reviews: Computational Molecular Science, 4(3), 169-181. https://doi.org/10.1002/wcms.1171 

9. Wacławek, S. (2021). Do we still need a laboratory to study advanced oxidation processes? A review of the modelling of radical reactions used for water treatment. Ecological Chemistry and Engineering, 28(1), 11-28. https://doi.org/10.2478/eces-2021-0002

10. Truhlar, D. G., & Garrett, B. C. (1980). Variational transition-state theory. Accounts of Chemical Research, 13(12), 440-448.

11. Libretexts. (2025, March 9). 30.10: The potential-energy surface can be calculated using quantum mechanics. Chemistry LibreTexts. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_%28LibreTexts%29/30%3A_Gas-Phase_Reaction_Dynamics/30.10%3A_The_Potential-Energy_Surface_Can_Be_Calculated_Using_Quantum_Mechanics

12. Mezei, M., & Beveridge, D. L. (1981). Theoretical studies of hydrogen bonding in liquid water and dilute aqueous solutions. The Journal of Chemical Physics, 74(1), 622-632.

13. Wilson, E. B., Decius, J. C., & Cross, P. C. (1980). Molecular vibrations: the theory of infrared and Raman vibrational spectra. Courier Corporation..

14. Bryce, D. L., Webster, F. X., Silverstein, R. M., & Kiemle, D. J. (2014). Spectrometric Identification of Organic Compounds.

15. Arrhenius, S. (1889). Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Zeitschrift für physikalische Chemie, 4(1), 96-116.