İkili Dizi Hizalaması: Genetik Farkları ve Benzerlikleri Ortaya Çıkarmak

DNA ve protein dizileri zaman içerisinde mutasyonla değişikliklere maruz kalırlar. Bu evrimsel veya çevresel mutasyonların araştırılması, tespiti veya evrimsel akrabalık, fonksiyonel benzerlik gibi biyolojik anlamlı bölgelerin araştırılması için iki veya daha fazla biyolojik dizi karşılaştırılır. Bu dizilerde tekil bazlar veya bazı kalıplar aranır. DNA veya kodladıkları protein dizilerinin alt alta sıralanması ve analiz edilerek çıkarımlar yapılması hizalama (alignment) olarak adlandırılmaktadır (1). Hizalama, karşılaştırılan dizi sayısına göre ikili ve çoklu dizi hizalama şeklinde ikiye ayrılır. İkili hizalama yalnızca iki dizinin benzerlik ilişkisini açıklar. Ayrıca hizalamanın kapsamına göre global ve yerel (local) olarak adlandırılan bir sınıflandırma bulunmaktadır (2). İlerleyen kısımlarda global ve lokal hizalama nedir ve hangi aşamalarda kullanılır gibi konulara değinilecektir. Önce hizalamanın nasıl yapıldığını, anlamlı sonuçlar elde ederken hangi kriterlere göre karar vereceğimizi görelim.

Hizalama işleminde iki dizinin uçlarından başlayarak bazların veya amino asitlerin eşleşme veya eşleşmeme durumlarına göre skorlamalar yapılır. Hizalamayı optimize etmek için boşluklar eklenebilir. Skorlama sistemi eşleşmelere + puan verirken eşleşmeyen karakterler cezalandırılarak skordan çıkarılır. Bu skorlamalar ile diziler arasındaki tüm olası hizalamaları temsil eden bir sayı matrisi üretilir ve matrisin en yüksek skorları optimal hizalamayı ifade etmektedir. Dinamik programla yöntemi en yüksek skorlu hizalamayı sağlayan bir yöntemdir (3).

Şekil 1. Örnek iki protein dizisinin hizalanması (3).

Daha karmaşık ve biyolojik olarak anlamlı karşılaştırmalar yapmak için substitusyon matrisleri kullanılır. En yaygın iki örnek olan PAM (Point Accepted Mutation) ve BLOSUM (Blocks Substitution Matrix) matrisleri, amino asitler arasındaki olası değişimlerin biyolojik olarak ne kadar olası olduğunu istatistiksel verilerle göstermektedir. Bu matrisler sayesinde sadece birebir eşleşmeler değil evrimsel olarak benzer amino asitler arasındaki değişimler de değerlendirilerek daha doğru hizalamalar yapılabilir (3).

Global hizalama, iki biyolojik dizinin tamamının uçtan uca karşılaştırıldığı bir hizalama türüdür. Bu algoritmada amaç, dizilerin tüm uzunluğu boyunca mümkün olan en iyi eşleşmeyi elde etmektir. Needleman-Wunsch algoritması, 1970 yılında geliştirilmiş ve bu amaç için kullanılan ilk dinamik programlama algoritmasıdır. Algoritma, bir skor matrisi oluşturarak, her hücredeki en iyi skoru önceki hücrelerden gelen olasılıkları değerlendirerek hesaplar. Skorlandırma; eşleşme, eşleşmeme ve boşluk cezaları üzerinden yapılır (3). Bu yöntem, diziler arasındaki optimum global hizalamayı garanti eder ancak diziler arasında çok sayıda örtüşmeyen bölge varsa biyolojik anlamlı sonuçlar üretmeyebilir. Yerel (local) hizalama ise yalnızca diziler arasında en çok benzeyen bölgenin hizalanmasını hedefler. Bu tür hizalama özellikle benzerlik taşıyan kısa motiflerin veya fonksiyonel alanların tespiti için uygundur. Smith-Waterman algoritması, 1981 yılında geliştirilmiştir. Yerel hizalama için en çok kullanılan dinamik programlama algoritmasıdır. Needleman-Wunsch algoritmasına benzer şekilde bir skor matrisi oluşturur ancak negatif skorlar sıfır olarak gösterilir ve yalnızca yüksek skorlu bölgeler takip edilir (3). Bu sayede, dizilerin geri kalan kısmı hizalamaya dahil edilmez ve lokal düzeyde biyolojik olarak anlamlı eşleşmeler elde edilir.

Şekil 2. DNA dizilerinin global ve yerel hizalamaları (2).

Dinamik programlama yöntemleri yüksek doğruluk sunsa da uzun dizilerde işlem süresi ve hafıza gereksinimi artar. Bu nedenle FASTA ve BLAST gibi daha hızlı ancak yaklaşık sonuçlar veren yöntemler geliştirilmiştir. FASTA’nın çalışma prensibi dizinin sabit uzunlukta kısa alt dizilere (k-tuples) bölünmesine dayanır. Bu alt diziler hedef verideki dizilerle eşleştirilir ve sonra ayrıntılı hizalama yapılır. BLAST ise sorgu dizisini kısa kelimelere bölerek veri tabanında tarama yapar. Eşleşen bölgeler uzatılır ve skor hesaplanır. Ardından yüksek skorlu eşleşmeler bulunur.

Needleman-Wunsch Algoritması

DNA ve protein dizilerini hizalamak için geliştirilen ilk ve önemli algoritmalardan biri, Needleman ve Wunsch tarafından 1970 yılında tanımlanmıştır (4). Bu algoritma, protein veya DNA dizilerinin hizalanmasında boşlukların (gap) eklenmesine izin vererek en uygun hizalamayı (optimal alignment) sağlaması açısından önemlidir. Sonuç optimaldir ancak tüm olası hizalamaların değerlendirilmesi gerekmez. Çünkü olası tüm çiftli karşılaştırmaları kapsayan kapsamlı bir analiz, hesaplama açısından çok pahalı (yani çok zaman ve işlem gücü gerektiren) olurdu (5).

Needleman–Wunsch algoritmasıyla yapılan global dizi hizalaması üç adımda açıklanabilir:

1. Bir matrisin kurulması

2. Matrisin puanlanması (scoring)

3. En uygun hizalamanın belirlenmesi

Adım 1 - Bir Matrisin Kurulması: İlk olarak, iki dizi iki boyutlu bir matriste karşılaştırılır (Şekil 3.). Uzunluğu m olan birinci dizi, x ekseni boyunca yatay olarak yerleştirilir; böylece bu dizideki amino asit rezidüleri sütunlara karşılık gelir. Uzunluğu n olan ikinci dizi ise, y ekseni boyunca dikey olarak yerleştirilir; bu dizideki amino asit rezidüleri satırlara karşılık gelir.

Şekil 3. İki amino asit dizisinin, Needleman ve Wunsch (1970) tarafından geliştirilen global hizalama için dinamik programlama algoritması kullanılarak ikili hizalanması. (a) İki dizi, matris boyunca çapraz bir yola yerleştirilebilir ve gerektiğinde bu yol yatay ya da dikey olarak sapabilir; bu sapmalar, hizalamaya boşlukların (gap) eklendiğini gösterir. (b) Birbirinin tamamen aynı olan iki dizi, matris üzerinde düz bir çapraz çizgiye oturan bir yol oluşturur. (c) Eğer eşleşmeyen bir durum (mismatch) – veya birden fazla – varsa, yol yine de genel olarak çapraz olarak devam eder; ancak bir puanlama sistemi, bu tür uyumsuzlukları cezalandırabilir (yani daha düşük puan verebilir). (d) Eğer hizalama birinci dizide boşluk içeriyorsa, yol dikey bir çizgi içerir. (e) Eğer hizalama ikinci dizide boşluk içeriyorsa, yol yatay bir çizgi içerir (5).

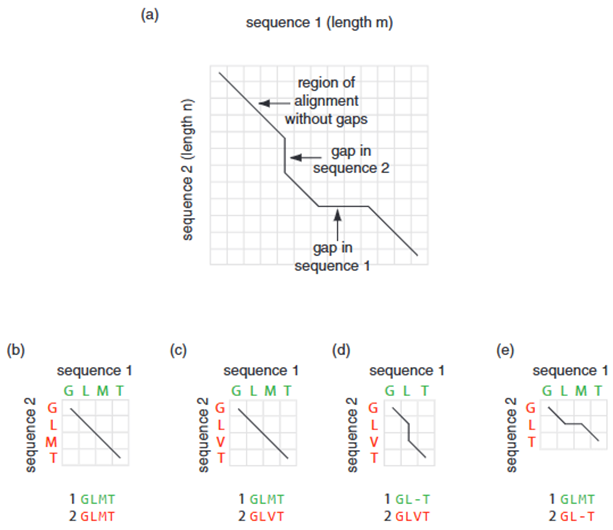
Birbirinin aynısı olan iki dizi arasındaki kusursuz bir hizalama, sol üst köşeden sağ alt köşeye doğru uzanan düz bir çapraz çizgiyle temsil edilir (Şekil 3 a, b). İki dizi arasında eşleşmeyen (mismatch) konumlar olsa bile bu hizalama yine çapraz bir yol üzerinde gösterilir (Şekil 3c.). Ancak bu tür eşleşmeler için verilen skor belirli bir puanlama sistemine göre ayarlanabilir. Örneğin, Şekil 3c.'deki V ve M rezidüleri arasındaki uyumsuzluk, Şekil 3b.'teki M ve M arasındaki mükemmel eşleşmeye kıyasla daha düşük bir skor alabilir. Eğer hizalama bir boşluk içeriyorsa, bu boşluk (d) birinci dizide yer alıyorsa yol dikey bir çizgi, (e) ikinci dizide yer alıyorsa yol yatay bir çizgi içerir. Alt dizideki herhangi bir boşluk, yatay bir çizgi olarak çizilir (Şekil 3., e). Bu boşluklar herhangi bir uzunlukta olabilir. Boşluklar iç kısımlarda ya da uç kısımlarda bulunabilir (5).

Adım 2 - Matrisin Puanlanması: Bu algoritmanın amacı, en uygun hizalamayı belirlemektir. Bunun için bir amino asit özdeşlik (identity) matrisi ve ardından bir puanlama (scoring) matrisi olmak üzere iki matris kurulur. Matrisin boyutları, ilk ve ikinci dizilere karşılık gelen x ve y ekseni boyunca (m + 1) × (n + 1) olacak şekilde oluşturulur (Şekil 4a.). Boşluk (gap) cezaları  (burada her boşluk pozisyonu için –2 değeri kullanılmıştır) ilk satır ve sütuna yerleştirilir. Bu, istenilen uzunlukta terminal boşlukların eklenmesine olanak tanımaktadır. Daha sonra, özdeşlik pozisyonları doldurulur (Şekil 4a., gri renkle doldurulmuş hücreler); buna özdeşlik matrisi (identity matrix) denir. İki dizi tamamen aynı olduğunda çapraz boyunca bir dizi gri dolu hücre yer alır. Ardından bir puanlama sistemi tanımlanır (Şekil 4b). En uygun hizalamayı bulmadaki hedef, matris boyunca skoru en yüksek olacak yolu belirlemektir. Bu, mümkün olan en fazla özdeşlik pozisyonunu içeren ve mümkün olan en az boşluğu barındıran bir yol bulmak anlamına gelir (5).

Şekil 4. Needleman ve Wunsch (1970) tarafından geliştirilen algoritma kullanılarak iki amino asit dizisinin global hizalaması için ikili hizalama örneği. (a) Uzunlukları m ve n olan diziler için, (m + 1) × (n + 1) boyutlarında bir matris oluşturulur. (b) Bu örnekte kullanılan puanlama sistemi, eşleşmeler (match) için +1, uyumsuzluklar (mismatch) için –2 ve boşluk cezaları (gap penalty) için de –2 puandır. (c) Her bir F(i, j) hücresinde, üç farklı yoldan elde edilen puan hesaplanır. Sol üst hücreden gelen yol (o hücrenin skoru + F(i, j)'nin puanı), solundaki hücreden gelen yol (boşluk cezası eklenir), üstündeki hücreden gelen yol (yine boşluk cezası eklenir). (d) İkinci satır ve ikinci sütundaki hücredeki puanı hesaplarken, +1, –4, –4 olan üç olasılıktan en yüksek olanı (+1) alınır. (f) Matrisin ilk satırına ait puanlar sırayla doldurulmaya devam edilir. (g) Tamamlanan matris, en uygun hizalamanın toplam skorunu içerir (–4; bu değer sağ alt köşedeki hücrededir ve her iki proteinin karboksil (C) ucuna karşılık gelir) (5).

Her bir i, j pozisyonunda (Şekil 4b.), dört olasılık vardır:

1. İki rezidü tam olarak eşleşebilir (yani özdeş olabilir); bu örnekte bu eşleşmeye +1 puan verilir.

2. Rezidüler eşleşmeyebilir (uyumsuz olabilir); bu durumda –2 puan verilir.

3. Birinci diziden bir boşluk (gap) eklenebilir; bu durumda –2 puan verilir.

4. İkinci diziden bir boşluk eklenebilir; bu da –2 puanla sonuçlanır.

Needleman ve Wunsch algoritması, hizalanan dizilerin her bir pozisyonu için bu olası durumların her birine karşılık gelen bir puan sağlar. Ayrıca, matris boyunca nasıl hareket edileceğini tanımlayan bir kural seti de sunmaktadır. Şekil 4c.'nin sağ alt köşesindeki hücre ele alındığında en uygun skora karar vermek için birkaç kural vardır:

1. İlk olarak hem i hem de j artmalıdır. Bu nedenle, belirli bir hücre F(i, j) için üç konumdan (üst, sol ve sol üst çapraz) gelen puanlar değerlendirilir. Bu, bir dizideki amino asitlerin (veya nükleotidlerin) doğrusal dizilimini ihlal etmemek için gereklidir.

2. Boşluklar (gap), istenilen sayıda pozisyona kadar uzatılabilir; puanlama sistemi, boşluk oluşturma ve boşluk uzatma için ayrı cezalar içerebilir.

3. Verilen özel puan, BLOSUM62 gibi bir puanlama matrisinden gelebilir.

Örnekteki iki diziyi hizalamaya başlarken, iki F rezidüsünün hizalanması sayesinde bir hücreye +1 değeri girilir (Şekil 4d.). Alternatif seçenekler (herhangi bir diziye boşluk eklemek) bir boşluk cezası gerektireceğinden daha düşük puanla sonuçlanır. Tercih edilen (en yüksek puanlı) yol, Şekil 4. boyunca kırmızı ok ile gösterilir. Sonra sağdaki bir sonraki hücreye geçilir ve -1 puan seçilir (sol hücreden gelmektedir: önceki hücreden +1, boşluk cezası –2 → toplam –1). Bu, diğer alternatif puanlar olan –4 ve –6’ya göre daha iyidir (Şekil 4e.).

Bu şekilde, her hücre için olası puanların analiz edilmesi süreci her satır boyunca devam eder (Şekil 4f.) ve sonunda tüm matris doldurulur (Şekil 4g.) (5).

Adım 3 - En Uygun Hizalamanın Belirlenmesi: Matris doldurulduktan sonra hizalama, iz sürme (trace-back) yöntemiyle belirlenir. Bu işleme, matrisin sağ alt köşesindeki hücreden başlanır (proteinler için karboksil uçları ya da nükleik asit dizileri için 3' ucu). Örnek için bu hücredeki puan –4’tür ve iki glutamat rezidüsünün hizalanmasına karşılık gelmektedir. Bu ve diğer tüm hücrelerde, en iyi puanın hangi üç komşu hücreden geldiği belirlenebilir. Bu süreç Şekil 5a.’da özetlenmiştir; kırmızı oklar, her hücrede en yüksek puanın geldiği yönü göstermektedir. Bu sayede gerçek hizalamaya karşılık gelen bir yol tanımlanır (turuncu renkli hücrelerle gösterilmiştir). Şekil 5b.'de, yalnızca her hücrede en iyi puanın hangi hücreden geldiğini gösteren oklar yer almaktadır. Bu, ikili hizalamanın en uygun yolunun alternatif bir şekilde tanımlanmasıdır (5).

Şekil 5. Dinamik programlama algoritması kullanılarak iki amino asit dizisinin global ikili hizalaması, matrisin puanlanması ve hizalamayı elde etmek için iz sürme (trace-back) yöntemiyle gerçekleştirilir. Şekil 4g.’deki hizalama gösterildiğinde, pembe renkle vurgulanan hücreler en uygun puanların kaynaklarını temsil eder. Eşdeğer bir gösterimde ise oklar, her hücrenin en iyi puanının geldiği hücreyi gösterir. Bu iz sürme işlemi, en uygun hizalamanın dizilimini belirlememizi sağlar. Dikey veya yatay oklar hizalamaya boşluk eklendiği pozisyonları; çapraz çizgiler ise birebir eşleşmeleri veya uyumsuzlukları temsil eder. Son skor olan –4, eşleşmelerin, uyumsuzlukların ve boşlukların toplam puanıdır. Bu örnekte 6 adet eşleşme vardır (6 × +1 = +6), uyumsuzluk yoktur, 5 adet boşluk ise toplam –10 puan getirir (5 × –2 = –10). Bu değerlerin toplamı –4 eder ve bu da hizalamanın toplam skorudur (5).

Bu yolla, her iki dizideki boşlukları da içerecek şekilde, karboksil uçtan amino uca doğru ilerleyerek hizalama oluşturulur. Elde edilen son hizalama (Şekil 5c.), kullanılan puanlama sistemine göre kesinlikle en uygun (optimal) olanıdır. Nadiren de olsa bazı durumlarda birden fazla hizalama aynı optimal skoru paylaşabilir ancak BLOSUM62 gibi puanlama matrisleri kullanıldığında bu durum oldukça nadir görülmektedir (5).

Smith-Waterman Algoritması

Smith ve Waterman (1981) (6) tarafından geliştirilen yerel hizalama (local alignment) algoritması, iki protein veya DNA dizisinin alt kümelerinin hizalanması için önemli yöntemlerden biridir. Yerel hizalama, özellikle sadece proteinlerin belirli bölgelerini (tüm diziler değil) hizalamak istenilen veri tabanı aramaları gibi çeşitli uygulamalarda son derece kullanışlıdır. Yerel dizi hizalama algoritması, global hizalamaya benzer şekilde çalışır: iki protein (veya DNA dizisi) bir matrise yerleştirilir ve çapraz boyunca en uygun yol aranır. Ancak, yerel hizalamada hizalamaya dizilerin iç kısımlarından başlanabilir ve hizalamanın dizilerin uçlarına kadar gitmesi gerekmez; yani başlangıç ve bitiş serbesttir. Smith–Waterman algoritması için, matrisin üst kısmına fazladan bir satır ve sol tarafına fazladan bir sütun eklenerek bir matris oluşturulur. Dizilerin uzunlukları m ve n olduğunda, matrisin boyutları (m + 1) × (n + 1) olur. Matrisin her bir pozisyonuna verilecek değerin kuralları, Needleman–Wunsch algoritmasında kullanılan kurallardan biraz farklıdır.

Her hücredeki puan, önceki çapraz hücreden gelen değer veya boşluk eklenmesiyle elde edilen değerler arasından en yüksek olanı olarak seçilir. Ancak Smith–Waterman algoritmasında önemli bir kural vardır. Skor hiçbir zaman negatif olamaz. Eğer tüm olasılıklar negatif bir değer veriyorsa ilgili hücreye sıfır (0) yazılır.

Yani, S(i,j) skoru şu dört olasılıktan en yükseği olarak tanımlanır:

1. (i – 1, j – 1) konumundaki hücreden gelen skor, yani sol üst çaprazdaki hücre. Bu skora, yeni konum olan s[i, j]’deki puan eklenir; bu puan bir eşleşme (match) veya uyumsuzluk (mismatch) olabilir.

2. S(i, j – 1), yani bir solundaki hücredeki skor; buna bir boşluk cezası çıkarılarak eklenir.

3. S(i – 1, j), yani yeni hücrenin hemen üstündeki skor; yine bir boşluk cezası çıkarılır.

4. Sıfır (0) sayısı (5).

Bu koşul, matris içerisinde negatif değerlerin bulunmamasını sağlamaktadır. Buna karşılık, boşluk (gap) veya uyumsuzluk (mismatch) cezaları nedeniyle global hizalamalarda negatif sayılar yaygın olarak görülür. Smith ve Waterman (1981) (6)'dan uyarlanarak iki nükleik asit dizisinin yerel hizalama algoritmasıyla hizalanmasına dair bir örnek Şekil 6.'da gösterilmiştir. Matrisin en üst satırı ve en sol sütunu sıfırlarla doldurulmuştur. Maksimum hizalama, matrisin herhangi bir yerinde başlayıp herhangi bir yerde bitebilir.

Şekil 6. (a) Bu örnekte, matris iki RNA dizisinden (CAGCCUCGCUUAG ve AAUGCCAUUGACGG) oluşturulmuştur. Bu bir özdeşlik matrisi değildir ancak nükleotid eşleşmelerinin olduğu konumlar gri (veya yerel hizalama bölgesinde pembe) ile renklendirilmiştir. Burada kullanılan puanlama sistemi şu şekildedir: eşleşme için +1, uyumsuzluk (mismatch) için eksi bir bölü üç (−1/3) ve boşluk (gap) cezası, eşleşme ile uyumsuzluk arasındaki farktır (1.3’lük boşluk cezası, boşluk uzunluğu 1 ise). Matris, dört olası negatif olmayan değerden en büyüğü bulunarak puanlanır. Matristeki en yüksek değer (3.3), optimal yerel hizalamanın başlangıç noktasıdır ve hizalanan nükleotitler (yeşil yazı ile gösterilen) yukarı ve sola doğru sıfır değerine ulaşıncaya kadar devam eder. (b) Bu matristen türetilen yerel hizalama gösterilmiştir. Bu hizalama; eşleşmeler, bir uyumsuzluk ve bir boşluk içerir. (c) Karşılaştırma amacıyla iki dizinin global hizalaması da gösterilmiştir. Bu hizalama, her iki dizinin tamamını kapsar (6).

İzlenecek yol, matristeki en yüksek değeri belirlemektir (Şekil 5a.’da bu değer 3.3’tür). Bu değer, hizalamanın bitiş noktasını temsil eder (nükleik asitler için 3' ucu veya proteinler için karboksil ucu). Bu konum, global hizalamalarda olması gerektiği gibi matriksin sağ alt köşesinde olmak zorunda değildir. İz sürme (trace-back) işlemi, bu en yüksek değerli hücreden başlayarak yukarı sola doğru çapraz olarak ilerler ve değeri sıfır olan bir hücreye ulaşana kadar devam eder. Bu nokta, hizalamanın başlangıcını tanımlar ve matriksin sol üst köşesinde olmak zorunda değildir.

İkili dizi hizalama, biyolojik diziler arasındaki benzerliklerin belirlenmesi ve bu benzerliklerin fonksiyonel, yapısal ya da evrimsel yorumlara dönüştürülmesi açısından biyoinformatiğin temel araçlarından biridir. Global ve yerel hizalama algoritmaları olan Needleman-Wunsch ve Smith-Waterman, yüksek doğruluk oranları ile referans yöntemler olarak kabul edilmektedir. Ancak veri hacminin büyümesiyle birlikte dotplot, FASTA ve BLAST gibi daha hızlı ve yöntemler, pratik uygulamalarda vazgeçilmez hâle gelmiştir. Tüm bu yöntemler, biyolojik verinin anlamlandırılmasında farklı ihtiyaçlara yanıt verirken doğru hizalama stratejisinin seçimi çalışmanın amacına, veri tipine ve kullanılabilir kaynaklara göre şekillenmelidir.

Referanslar

1. Haubold, B., & Wiehe, T. (2006). Introduction to computational biology: An evolutionary approach. Birkhäuser Verlag.

2. Diniz, W. J. S., & Canduri, F. (2017). Bioinformatics: An overview and its applications. Genetics and Molecular Research, 16(1), gmr16019645. https://doi.org/10.4238/gmr16019645

3. Mount, D. W. (2004). Bioinformatics: Sequence and genome analysis (2nd ed.). Cold Spring Harbor Laboratory Press.

4. Needleman, S. B., & Wunsch, C. D. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of molecular biology, 48(3), 443–453. https://doi.org/10.1016/0022-2836(70)90057-4

5. Jonathan Pevsner. (2009). Bioinformatics and Functional Genomics. John Wiley & Sons, Inc. https://doi.org/10.1002/9780470451496

6. Smith, T. F., & Waterman, M. S. (1981). Identification of common molecular subsequences. Journal of molecular biology, 147(1), 195-197.