Schrödinger Equation and Atomic Orbitals

Understanding the electronic structure of atoms and molecules is one of the cornerstones of modern chemistry and drug design. The Schrödinger equation, developed to describe these structures, lies at the heart of quantum chemistry and forms the foundation of computational chemistry approaches. In this article, we explore quantum chemical calculations on molecules, beginning with the theoretical foundations of the Schrödinger equation, moving on to atomic orbitals, and ultimately addressing molecular systems.

Foundations of the Schrödinger Equation

Developed in 1926 by Erwin Schrödinger, the quantum wave equation is used to describe the behavior of particles such as electrons, which cannot be explained by classical mechanics.

In its time-independent form, the Schrödinger equation is expressed as follows (1):

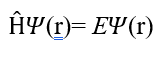
The following terms appear in the equation:

H: The Hamiltonian operator, which represents the total energy of the system (kinetic + potential energy).

Ψ: The wave function, which gives the probability amplitude depending on the particle’s position in space.

E: The energy value, representing the quantized energy level of the system.

For an electron, the Hamiltonian can be written as follows:

This equation can be solved analytically for single-electron systems such as the hydrogen atom. For more complex systems, however, numerical approaches are required.

Atomic Orbitals and Quantum Numbers

Analytical solutions of the Schrödinger equation for the hydrogen atom yield wave functions known as atomic orbitals.These orbitals define the probability distribution of an electron in space. Solving the Schrödinger equation in spherical coordinates allows us to separate these functions into radial and angular components:

Rₙ,ₗ(r): Radial wave function

Yₗ,ₘ(θ,ϕ): Spherical harmonics (angular component)

This expression provides not only the value of the electron density at a single point, but also its overall spatial structure (2).

Meaning of Quantum Numbers

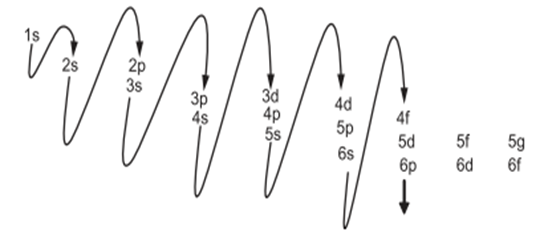
Orbitals are defined by the following four quantum numbers:

Principal quantum number (n): Indicates the energy level of the electron. It affects the electron’s average distance from the nucleus. As n increases, the size of the orbital increases. Angular momentum quantum number (l): Determines the geometric shape of the orbital.

l = 0: s orbital (spherical)

l = 1: p orbital (lobed)

l = 2: d orbital (flower-like)

l = 3: f orbital (more complex)

Magnetic quantum number (mₗ): Describes the orientation of the orbital in space. mₗ can take integer values ranging from –l to +l. Spin quantum number (mₛ): Specifies the direction of the electron’s intrinsic spin. mₛ can have a value of +½ or –½.

Figure 1. Orbital Energies with Increasing Atomic Number (3)

Approximate Methods

Since an analytical solution to the Schrödinger equation is not possible for real molecules, approximate numerical methods are used. These methods form the foundation of quantum chemical calculations:

Hartree-Fock (HF) Approach

This approach is based on the assumption that each electron experiences the average potential created by all other electrons.The total wave function of the system is expressed as a Slater determinant of single-electron orbitals.Each electron interacts with the others through an average field. Its advantage lies in its simplicity, while its main disadvantage is that it does not adequately account for electron-electron correlation.Nevertheless, it is commonly used as a starting point for many systems (4).

Figure 2. An Example Slater Determinant for the Hartree-Fock Approach (5).

Density Functional Theory (DFT)

DFT calculates the energy of a system based on electron density. The fundamental principle is that the electron density determines all of the system's essential properties. Quantum systems are modeled using this density instead of a single wave function. Thanks to modern functional sets (such as B3LYP, PBE, etc.), DFT allows efficient and fast calculations even for multi-core systems. In silico, many parameters like molecular geometry optimization, electron distribution, and reaction coordinates are obtained using DFT. DFT is particularly popular in fields such as drug design and materials science due to its success in balancing computational time and accuracy. This probability density forms the basis for the creation of chemical bonds. The phase-aligned interaction of two atomic orbitals creates a bonding orbital, while out-of-phase interaction leads to an anti-bonding orbital. This phenomenon enables the understanding of covalent bond formation and the stability of molecules at the quantum level. Additionally, this information is used in the molecular modeling of ligand-receptor interactions. Electron density maps based on the Schrödinger equation are essential for understanding how drug molecules interact with their target proteins (6).

References

1. Griffiths, D. J. (2005). Introduction to Quantum Mechanics. Pearson Education.

2. Atkins, P., & Friedman, R. (2011). Molecular Quantum Mechanics. Oxford University Press.

3. S. Ekambaram. (2012). General Chemistry. Pearson Education India.

4. Szabo, A., & Ostlund, N. S. (1996). Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover Publications.

5. Errol G. Lewars. (2010). Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Springer Science & Business Media.

6. McQuarrie, D. A. (2008). Quantum Chemistry. University Science Books.