From Atomic Theories to Atomic Orbitals: The Big Story of Tiny Particles

Classical Atomic Theory

The concept of the atom was first developed by ancient Greek philosophers. It is believed that Leucippus was the first to propose an atomic hypothesis around 500 BCE, which was greatly expanded upon by Democritus. The renowned philosopher Aristotle, who developed the four-element theory, opposed the idea of atoms because he rejected the principle of the void. Aristotle's prestige was so great that his views overshadowed Democritus' theory, causing atomic theory to fall out of favor for nearly 2,000 years (1).

Figure1. A depiction of Democritus (created using AI).

The atomic theory, as we know it today, was shaped in the mind of Dalton. Dalton began his scientific work as a meteorologist, studying the properties of the atmosphere. In 1801, he explained the law of partial pressures in a paper, stating that the total pressure of a gas mixture is the sum of the partial pressures exerted by each gas.

Dalton's atomic theory proposed the following:

1. Elements are made of small, indivisible particles called atoms.

2. All atoms of a given element are identical in size and weight.

3. Atoms of two or more different elements combine to form compounds. Each compound is composed of the same type of atoms in the same ratio.

4. Chemical reactions involve the rearrangement, separation, or combination of atoms. Atoms are neither created nor destroyed in chemical reactions.

Dalton’s postulates remained the guiding principles of chemistry for over 100 years. However, some of Dalton’s explanations have been modified. We now know that atoms of the same element are not completely identical to each other and are made up of smaller particles. However, an atom is still considered the smallest particle that retains the properties of an element. Although atoms are the building blocks of everything around us, we cannot see one atom or billions of atoms with the naked eye. However, when billions of atoms come together, the properties of each atom combine with the properties of the next atom and we begin to see the properties we associate with the element (3).

In the early 19th century, scientists discovered that gases could conduct electricity by experimenting with gas discharge tubes (also known as cathode ray tubes). These tubes were glass tubes from which almost all the gas had been removed under vacuum and then sealed. Electrodes were placed at each end of the tube, and when current was applied to the electrodes, a beam of charged particles (cathode rays) was produced, which was observed as a bright spot on a detector screen. In 1897, John J. Thomson designed an experiment using cathode ray tubes. He used a perforated electrode to force the cathode ray out of the tube and studied how the cathode ray behaved when exposed to externally charged plates and a magnetic field (4). Thomson was able to balance the deflection by adjusting the charges on the plates and the strength of the magnetic field and calculated the charge-to-mass ratio of the particles forming the cathode rays. The charge-to-mass ratios he calculated were surprisingly large, indicating that the mass of the particles in the cathode rays was very small. Thomson described these particles as having "an insignificant fraction of the mass of the hydrogen atom." Then, in 1904, J. J. Thomson proposed a model called the "plum pudding model", which suggested that the atom was composed of a sphere of positively charged matter, inside which were electrons, which were negatively charged particles. This model resembled a structure similar to grapes scattered in a cake (5) (Figure 2).

Figure 2. Image showing J. J. Thomson's grape cake model. The atomic model depicts negatively charged electrons as "grapes" scattered in a "cake" of positive charges (3).

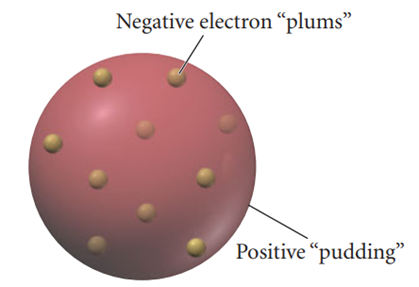
In J.J. Thomson’s atomic model, in the ground state of the atom, electrons are fixed in their equilibrium positions and emit no radiation. In the excited state of the atom, electrons oscillate around their equilibrium positions and emit radiation by dipole oscillations because they are constantly accelerating and decelerating due to the charge they carry (6).

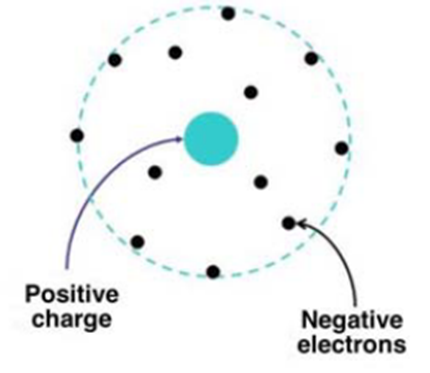
In contrast to Thomson’s “raisin cake” atomic model, according to Rutherford’s atomic model, the entire mass of the atom is concentrated in the atomic nucleus, where the positive charge is also located, and the radius of the nucleus is about 10⁻¹⁵ m. The electrons are distributed around the atom in a spherical cloud with a radius of about 10⁻¹⁰ m (Figure 3).

Figure 3. According to Rutherford’s atomic model, electrons revolve around a positively charged nucleus, which contains most of the atom’s mass, in an empty space (6).

Rutherford conducted a series of experiments to develop his atomic model. Rutherford conducted an experiment with alpha particles (basically positively charged particles) and directed these particles at a thin metal foil. Interestingly, while some alpha particles were deflected by the dashed lines as shown in Figure 4, most particles passed through the foil as shown by the arrow. In this case, both deflected and passing alpha particles were detected. The results of these experiments show that most of the alpha particles passed through the metal foil, confirming that the atoms of the thin metal have largely empty space (7). However, the deflection of some of the alpha particles suggests that the atoms of the metal have a small, dense positively charged space (8).

Figure 4. Rutherford's experimental setup using thin metal foil (8).

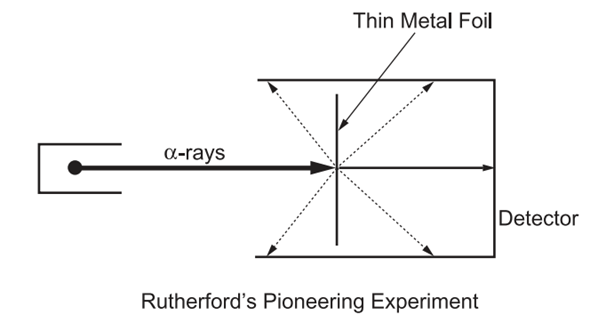
Rutherford's reaction to this discovery after the experiment was as follows: "It was as incredible as shooting a 15-inch cannonball at a thin piece of tissue paper and having it come back and hit you." According to Rutherford's atomic model;

• The atom is mostly empty space, so most α particles can pass through without any deflection.

• The positive charge and mass of the atom are concentrated in the nucleus, which is a very dense and small region.

• When an α particle approaches the nucleus, it feels a strong repulsion force and can be scattered at large angles.

• If an α particle is aimed directly at the nucleus, it can be completely bounced back by a huge repulsion force.

Later, the positively charged particles in the nucleus were called "protons". Other experiments found that the charge of a proton was equal to that of an electron but opposite in sign, and that the mass of a proton was about 1.67262 × 10⁻²⁴ g, or about 1840 times heavier than the mass of an electron (9). However, Rutherford's model created a major theoretical problem. According to the classical electromagnetic theory accepted at the time, a charged particle (such as an electron) spinning around the center must constantly lose energy by emitting electromagnetic radiation. In this case:

• The electron loses energy rapidly

• Falls into the nucleus in a spiral path

• The atom collapses in about 10⁻¹⁰ of a second.

• This theory could not explain why the atom had a stable structure.

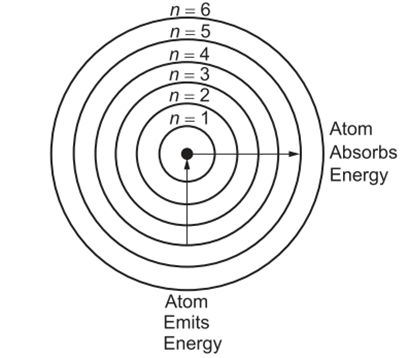
The Danish physicist Niels Bohr solved this impasse in 1913. Working with Rutherford at the time, Bohr developed a new atomic model using the quantum theory of Max Planck and Albert Einstein (10). Niels Bohr provided a theoretical explanation for the emission spectrum of the hydrogen atom with his work (11). According to the laws of classical physics, the electron in the hydrogen atom must constantly emit energy in the form of electromagnetic waves as it accelerates towards the nucleus. To explain this situation, Bohr proposed that electrons can only exist at certain energy levels. Bohr's basic assumptions are as follows:

• Electrons can only exist in certain energy levels (orbits). Their energy is quantized, meaning they cannot take on a random energy value.

• An electron does not emit energy while moving in a certain orbit, so it does not fall into the nucleus.

• Electrons move to different orbits when they absorb or emit energy.

•  An electron that moves from a higher energy orbit to a lower energy orbit emits a photon (a particle of light).

This process explains the formation of lines in the hydrogen spectrum (9). Bohr showed that the energy levels that an electron in a hydrogen atom can have can be expressed by the following equation.

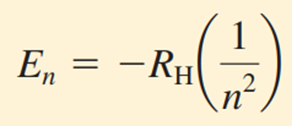
Here, RH is the Rydberg constant (named after the Swedish physicist Johannes Rydberg) and its value is 2.18×10−18 J. The number n is called the principal quantum number and can take integer values ​​such as 1, 2, 3. The negative sign in the equation shows that the energy of an electron in an atom is lower than the energy of a free electron infinitely far from the nucleus. The energy of a free electron is considered zero. Mathematically, this corresponds to setting the value of 𝑛 equal to infinity in the equation, i.e. 𝐸∞=0. As the electron approaches the nucleus (𝑛 decreases), the value of 𝐸𝑛 increases in absolute terms, but also becomes more negative. The most negative value is obtained when 𝑛=1, which means the most stable energy level. This state is called the ground state and represents the lowest energy level of a system. For values ​​of 𝑛=2,3,… the stability of the electron decreases. Each of these levels is called an excited state and has a higher energy than the ground state. A hydrogen electron with 𝑛 > 1 is considered to be in an excited state (9).

According to Bohr’s model, the radius of each orbit is proportional to 𝑛2. Therefore, as we go from 𝑛=1 to 𝑛=2,3, the radius of the orbit increases rapidly. The higher the energy level the electron is in, the farther the electron is from the nucleus and the weaker it is held by the nucleus. Bohr’s theory allows us to explain the line spectrum of the hydrogen atom. The energy of the radiation absorbed by the atom causes the electron to transition from a lower energy state (smaller 𝑛 value) to a higher energy state (larger 𝑛 value). Conversely, when an electron moves from a higher energy level to a lower energy level, radiant energy is emitted in the form of a photon.

Figure 5. Bohr Model of the Hydrogen Atom, Where n = Principal Quantum Number, 1,2,3,4, . . . (8).

Quantum Mechanics

Quantum mechanics is a much more powerful theory that provides significant advances beyond the Bohr atomic model. While Bohr’s atomic model was successful in explaining simple systems such as the hydrogen atom, quantum mechanics provides a much wider range of accurate and detailed explanations. The Schrödinger equation specifies the possible energy states that an electron in a hydrogen atom can enter and defines the corresponding wave functions (ψ) (12). These energy states and wave functions are characterized by a set of quantum numbers, and with these numbers a comprehensive model of the hydrogen atom can be constructed. Although quantum mechanics says that we cannot precisely locate an electron in an atom, it does define the region where the electron can be found at a given time. The concept of electron density gives the probability of finding an electron in a particular region of the atom. The square of Schrödinger’s wave function (ψ²) describes the distribution of electron density in three-dimensional space around the nucleus. Regions of high electron density indicate a high probability of finding an electron, while regions of low electron density indicate a low probability of finding an electron (9).

To distinguish the quantum mechanical description of an atom from the Bohr model, the term atomic orbitals is used instead of orbits. An atomic orbital can be thought of as the wave function of an electron in an atom. An atomic orbital has a specific energy and a specific distribution of electron density. While the Schrödinger equation works well for the simple hydrogen atom, which has a single proton and one electron, it cannot be solved exactly for atoms containing more than one electron. However, chemists and physicists have developed approximate solutions to overcome such difficulties. For example, although the behavior of electrons in multi-electron atoms (atoms with two or more electrons) is different from that in the hydrogen atom, it is assumed that the difference is not very large. Therefore, the energy and wave functions obtained from the hydrogen atom can be used as good approximations of the behavior of electrons in more complex atoms (9).

Atomic Orbital Types

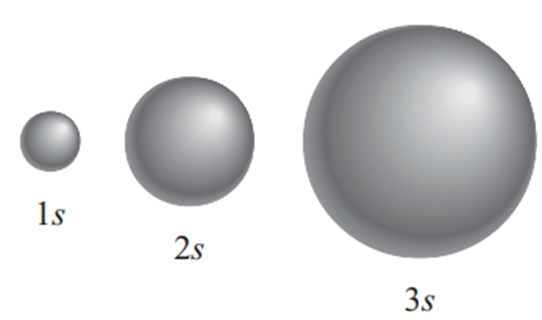
s orbital

The ‘s’ orbital has a spherical shape. The center of the sphere is the nucleus, and electrons are located at a certain distance. Therefore, as the principal quantum number (n) increases, the shape of the orbitals becomes increasingly larger (8).

Figure 6. Boundary surface diagrams of hydrogen 1s, 2s and 3s orbitals (9).

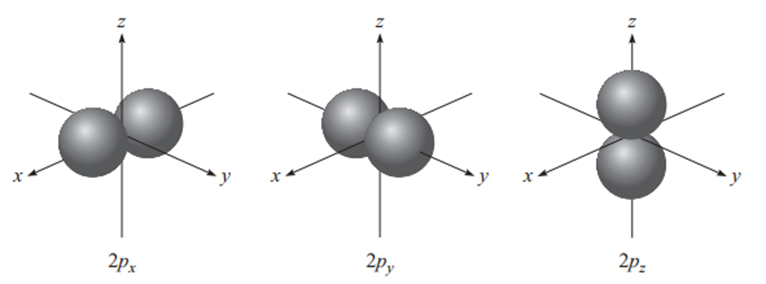
p orbital

When ℓ=1, the magnetic quantum number (mℓ)​ can take on the values ​​-1, 0, and 1. Therefore, when n = 2 and ℓ=1, three 2p orbitals are formed, 2px, 2py, and 2pz. The letter subscripts indicate the axes along which the orbitals are oriented. These three p orbitals are identical in size, shape, and energy; they differ only in their orientation (9).

Figure 7. Boundary surface diagrams of the three 2p orbitals (9).

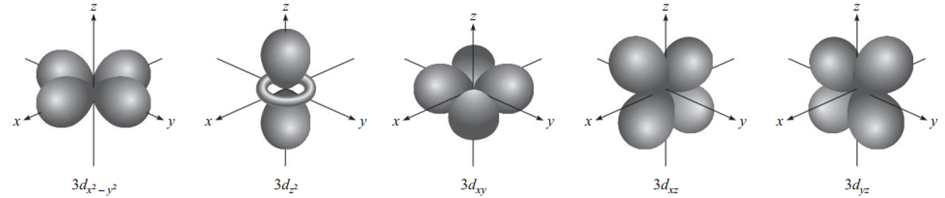
d orbital

When ℓ=2, there are five mℓ​ values ​​(-2, -1, 0, 1, 2) corresponding to the five d orbitals. The lowest n value of a d orbital is 3. Because ℓ can never be greater than n−1, so when n=3 and ℓ=2, there are five 3d orbitals (3dxy, 3dyz, 3dxz, 3dx²-y² and 3dz²). As with the p orbitals, different orientations of the d orbitals correspond to different values ​​of mℓ​, but there is still no direct relationship between a given orientation and a particular mℓ​ value. All 3d orbitals in an atom are identical in terms of their energies. The d orbitals with n values ​​greater than 3 (4d, 5d, ...) have similar shapes (9).

Figure 8. Boundary surface diagrams of five 3D orbitals.

Orbitals with higher energies than the d orbitals are labeled f, g, ... etc. The f orbitals are important for explaining the behavior of elements with atomic numbers greater than 57, but they are difficult to represent in shape (9).

Our knowledge of the structure of the atom has evolved greatly with scientific developments. Starting with Dalton's atomic model, the understanding of the atom expanded with the discoveries of Thomson and Rutherford, and has been further deepened by Bohr's quantum leaps and the wave functions provided by modern quantum mechanics. Today, thanks to the Schrödinger equation, we can determine atomic orbitals by defining the probability distribution of electrons. These developments have not only helped us understand the structure of the atom, but have also opened the door to revolutionary advances in many fields, from chemistry to materials science, from drug development to nanotechnology. The journey to understanding the nature of the atom continues to be an endless process of discovery for scientists.

REFERENCES

1. Peacocke, T. A. H. (1967). Atomic and Nuclear Chemistry: Atomic Theory and Structure of the Atom. Pergamon.

2. Dalton, John. (1801). Experimental essays, on the constitution of mixed gases; on the force of steam or vapour from water and other liquids in different temperatures, both in a Torricellian vacuum and in air; on evaporation; and on the expansion of gases by heat. Memoirs of the Literary and Philosophical Society of Manchester, 5(2), 535--602. https://www.biodiversitylibrary.org/part/308525

3. Karen C. Timberlake. (2011). Chemistry: An Introduction to General, Organic, and Biological Chemistry (11th Edition). Pearson.

4. Thomson, J. J. (1897). XL. Cathode Rays. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 44(269), 293–316. https://doi.org/10.1080/14786449708621070 

5. Susan Young, William Vining, Roberta Day, Beatrice Botch. (2017). General Chemistry Atoms First. Cengage Learning.

6. Podgoršak, E. B. (2006). Rutherford—Bohr Atomic Model. Radiation Physics for Medical Physicists, 42-85.

7. Rutherford, E. (1911). "The Scattering of α and β Particles by Matter and the Structure of the Atom." Philosophical Magazine, 21(125), 669-688. https://doi.org/10.1080/14786440508637080  

8. S. Ekambaram. (2012). General Chemistry. Pearson Education India.

9. Raymond Chang, Jason Overby. (2011). General Chemistry: The Essential Concepts. McGraw-Hill.

10. Darrell Ebbing, Steven D. Gammon. (2007). General Chemistry: Media Enhanced Edition. Cengage Learning.

11. Bohr, N. (1913). "On the Constitution of Atoms and Molecules." Philosophical Magazine, 26(151), 1-25. https://doi.org/10.1080/14786441308634955 

12. Schrödinger, E. (1926). "Quantisierung als Eigenwertproblem" (Quantization as an Eigenvalue Problem). Annalen der Physik, 79(4), 361-376. https://doi.org/10.1002/andp.19263840404