Molecular Orbital Theory: Discovering Chemical Bonds with Quantum Mechanics

Molecular orbital theory is a basic quantum mechanics approach that explains how atoms bond to form molecules and how electrons are distributed within these bonds. This theory proposes that atomic orbitals combine to form molecular orbitals, and that these orbitals determine the probability density of electrons. Molecular orbital theory, which plays a critical role in understanding the strength, magnetic properties, and electronic transitions of molecular bonds, is widely used, especially in explaining the mechanisms of chemical reactions and spectroscopic properties. This article will discuss the basic principles of molecular orbital theory, its effect on bond formation, and how it is applied in computational chemistry.

Molecular orbital theory explains covalent bonds in terms of molecular orbitals, which are formed by the interaction of the atomic orbitals of the bonding atoms and are associated with the entire molecule. The difference between a molecular orbital and an atomic orbital is that an atomic orbital is associated with only one atom, whereas a molecular orbital is spread over the entire molecule. According to molecular orbital (MO) theory, the overlapping of the 1s orbitals of two hydrogen atoms results in the formation of two molecular orbitals, a bonding molecular orbital and an antibonding molecular orbital. The bonding molecular orbital has lower energy and higher stability than the atomic orbitals that form it. The antibonding molecular orbital, on the other hand, has higher energy and lower stability than the atomic orbitals. As the terms "bonding" and "antibonding" indicate, the placement of electrons in the bonding molecular orbital results in a stable covalent bond, while the placement of electrons in the antibonding molecular orbital results in an unstable bond.

In bonding molecular orbitals, the electron density is highest between the nuclei of the bonding atoms. In antibonding molecular orbitals, the electron density drops to zero between the nuclei. To understand this difference, it is necessary to remember that electrons in orbitals have wave properties. A unique property of waves is that waves of the same type interact with each other, causing either their amplitude to increase or decrease. The formation of bonding molecular orbitals corresponds to constructive interference (an increase in amplitude is similar to an increase in the electron density between two nuclei). The formation of antibonding molecular orbitals corresponds to destructive interference (a decrease in amplitude is similar to a decrease in the electron density between two nuclei) (1). Therefore, the constructive and destructive interactions of the two 1s orbitals in the H₂ molecule result in the formation of a sigma bonding molecular orbital (σ1s) and a sigma antibonding molecular orbital (σ*1s) (Figure 1).

Figure 1. Relative energies of the 1s orbital of the H atom and the σ1s and σ*1s molecular orbitals of the H₂ molecule (2).

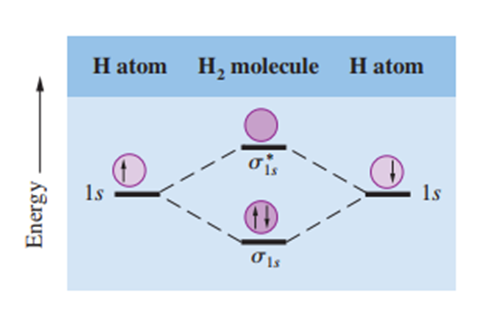
Sigma Molecular Orbitals

In a sigma molecular orbital (bonding or antibonding), the electron density is concentrated symmetrically along a line between the two nuclei of the bonding atoms. Two electrons in a sigma molecular orbital form a sigma bond. A single covalent bond (for example, H–H or F–F) is almost always a sigma bond.

The molecular orbital energy level diagram showing the relative energy levels of the orbitals produced during the formation of the H₂ molecule and the constructive and destructive interactions of the two 1s orbitals is shown in Figure 1. In the antibonding molecular orbital, there is a node between the nuclei where the electron density is zero. In this case, the nuclei are repelled by each other's positive charges and are not held together. Electrons in antibonding molecular orbitals have higher energy (and lower stability) than electrons in isolated atoms. On the other hand, electrons in bonding molecular orbitals have lower energy (and therefore higher stability) than electrons in isolated atoms (1).

Pi Molecular Orbitals

In a pi molecular orbital (bonding or antibonding), the electron density is concentrated above and below the line connecting the two nuclei of the bonding atoms. Two electrons in a pi molecular orbital form a pi bond. Double bonds almost always consist of one sigma bond and one pi bond, while triple bonds always consist of one sigma bond and two pi bonds.

Figure 2. Relative energies of molecular orbitals of homonuclear diatomic molecules and the resulting sigma and pi molecular orbitals.

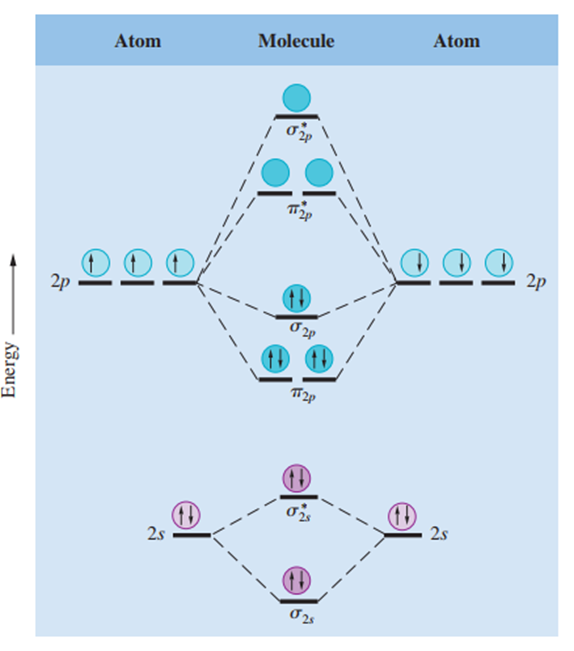
The Role of Molecular Orbitals in Chemical Reactions

Molecular orbitals (MOs) play a critical role in understanding the mechanisms of chemical reactions. When the distribution of electrons in a molecule is examined using molecular orbital theory, important clues are obtained about how the reaction will proceed. In particular, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) interactions are the main factors that determine the probability of reactions. HOMO determines the nucleophilic properties of a molecule, while LUMO determines its electrophilic properties. This approach, known as Frontier Molecular Orbital Theory (FMOT), is widely used to explain the mechanisms of many organic chemical reactions such as Diels-Alder reactions, electrophilic aromatic substitutions, and organocatalysis. In addition, thanks to density functional theory (DFT) calculations performed with quantum chemistry techniques, the orbital energies of reactants and products and transition states can be examined in detail. Such calculations are used to optimize reaction efficiency and mechanisms in a wide range of fields, from drug design to materials science (3).

Figure 3. HOMO – LUMO orbitals of the tolcapone molecule (4).

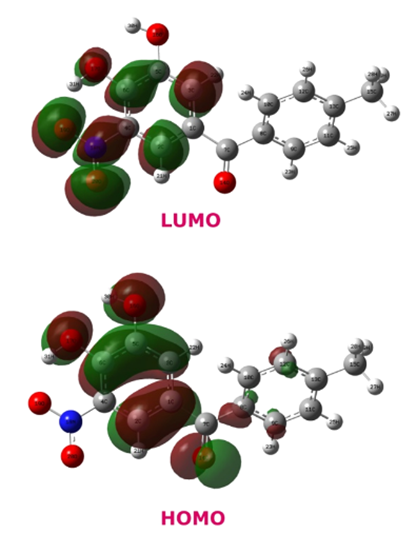
Molecular orbitals are also used to study the transition states of chemical reactions. Quantum chemistry techniques, especially Density Functional Theory (DFT) and Hartree-Fock methods, help us understand energy barriers and the structures of unstable intermediates by modeling reaction coordinates. For example, pericyclic reactions (Diels-Alder, electrocyclization) and radical processes can be predicted using molecular orbital symmetry (Woodward-Hoffmann Rules). Molecular orbitals also have a great effect in biological systems. In enzyme-catalyzed reactions, HOMO-LUMO interactions between the substrate and the enzyme active site direct the bond-making and breaking processes. At the same time, in the fields of photochemistry and quantum biology, biological processes (e.g. photosynthesis and the mechanism of vision) can be explained by orbital changes of electrons excited by light. These theoretical concepts find practical applications in disciplines such as drug design, catalysis, nanotechnology and materials science. Molecular orbital calculations are used to understand how new drug molecules interact with biomolecules and provide important guidance in the design of π-conjugated systems in organic electronics. As a result, molecular orbitals are a powerful tool for explaining the fundamental mechanisms of chemical reactions and have wide applications in many areas of modern chemistry and biochemistry (5,6).

REFERENCES

1.  Raymond Chang, Jason Overby. (2011). General Chemistry: The Essential Concepts. McGraw-Hill.

2. Darrell Ebbing, Steven D. Gammon. (2007). General Chemistry: Media Enhanced Edition. Cengage Learning.

3. Fukui, K. (1982). Role of frontier orbitals in chemical reactions. science, 218(4574), 747-754.

4. Isravel, A. D., Jeyaraj, J. K., Thangasamy, S., & John, W. J. (2021). DFT, NBO, HOMO-LUMO, NCI, stability, Fukui function and hole–Electron analyses of tolcapone. Computational and Theoretical Chemistry, 1202, 113296.

5. Woodward, R. B., & Hoffmann, R. (1969). The Conservation of Orbital Symmetry. Angewandte Chemie International Edition, 8(11), 781-853. https://doi.org/10.1002/anie.196907811 

6. Parr, R. G., & Yang, W. (1989). Density-Functional Theory of Atoms and Molecules. Oxford University Press.